Question

Steve can afford a $330 per month car payment. If he is being offered a 6 year car loan with an APR of 1.2%, compound monthly, what is the value of the most expensive car he can afford?

Answer 1

Answer:22,913.76

Explanation:

Answer 2

The value of most expensive car he can afford is $ 22913.757.

Explanation:

Since, the periodic payment of a loan is,

`P=(r(PV))/(1-(1+r)^(-n))`

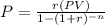
Where, P.V. is the presents value of the loan,

r is the rate per period,

n is the number of periods,

Here, Monthly payment, P = $ 330,

⇒ The loan is compound monthly,

Thus, if the time = 6 years,

The number of periods, n = 6 × 12 = 72 months, ( 1 year = 12 months ),

Also, the A.P.R = 1.2 % = 0.012

So, the rate per periods,

`r=(0.012)/(12)`

By substituting the values,

`330=((0.012)/(12)(PV))/(1-(1+(0.012)/(12))^(-72))`

`\implies x = $ 22913.757`

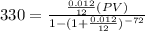
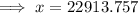
Hence, the value of most expensive car he can afford is $ 22913.757.