Question

Parallelogram CARD has vertices (5, -2), (-1, -2), (1, 2), and (7, 2), respectively. The diagonals, CR and AD intersect at Point T. What is the length of CT? What is the length of DT?

Complete your work in the space provided or upload a file that can display math symbols if your work requires it. If necessary, round lengths to the nearest hundredth of a unit.

Answer 1

a) T(3,0)

b) |CT|=2.83

c) |DT|=4.47

Explanation:

The given parallelogram CARD has vertices (5, -2), (-1, -2), (1, 2), and (7, 2)

The diagonals of a parallelogram bisect each other.

Find the midpoint of one diagonal, that gives us the point of intersection of the diagonals T.

The midpoint of C(5,-2) and (1,2) is

`T((5+1)/(2),(-2+2)/(2)  )`

`T(3,0)`

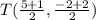
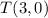
b) To find the length of CT, we use the distance formula; where C(5,-2) ahd T(3,0).

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

`d=√((3-5)^2+(-2-0)^2)`

`d=√(4+4)`

`d=√(8)`

`d=2√(2)=2.83`

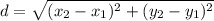
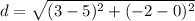
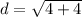
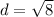
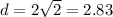
The length of CT is 2.83 to the nearest hundredth

c) To find the length of DT, we use the distance formula; where D(7,2) ahd T(3,0).

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

`d=√((3-7)^2+(2-0)^2)`

`d=√(16+4)`

`d=√(20)`

`d=2√(5)=4.47`

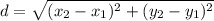
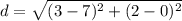
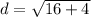
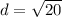
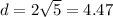
The length of DT is 4.47 to the nearest hundredth