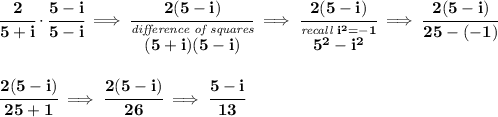Question

What is the completely simplified equivalent of 2/(5+i)?

A. (5-i)/12
B. (5+i)/12
C. (5-i)/13
D. (5+i)/13

Please explain how you got your answer too!

Answer 1

namely, let's rationalize the denominator in the fraction, for which case we'll be using the conjugate of that denominator, so we'll multiply top and bottom by its conjugate.

so the denominator is 5 + i, simply enough, its conjugate is just 5 - i, recall that same/same = 1, thus (5-i)/(5-i) = 1, and any expression multiplied by 1 is just itself, so we're not really changing the fraction per se.

`\bf \cfrac{2}{5+i}\cdot \cfrac{5-i}{5-i}\implies \cfrac{2(5-i)}{\stackrel{\textit{difference of squares}}{(5+i)(5-i)}}\implies \cfrac{2(5-i)}{\stackrel{\textit{recall }i^2=-1}{5^2-i^2}}\implies \cfrac{2(5-i)}{25-(-1)} \\\\\\ \cfrac{2(5-i)}{25+1}\implies \cfrac{2(5-i)}{26}\implies \cfrac{5-i}{13}`