The circle described by the equation (x-3)^(2) +(y+4)^(2)=9 is translated 5 units to the left and 1 unit up. At what point is the center of the image circle located? (-8,5) (-2,…

Question

The circle described by the equation
`(x-3)^(2) +(y+4)^(2)=9` is translated 5 units to the left and 1 unit up.

At what point is the center of the image circle located?


(-8,5)

(-2,-3)

(2,-3)

(8,-5)

Answer 1

hello : ( -2 ; - 3)

Explanation:

the center is A( 3 ; - 4)

translated :

5 units to the left : 3 -5 = -2

1 unit up: -4+1 = -3

the point is the center of the image circle located: B(-2 ; - 3)

Answer 2

The point at which center of the image circle located is (-2, -3) so second option is correct.

Explanation:

Given equation of circle is:

`(x-3)^(2) + (y+4)^(2) = 9` (i)

The general equation of circle is mentioned below,

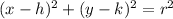`(x-h)^(2) + (y-k)^(2) = r^(2)` (ii)

Here 'r' represents the radius of the circle and (h,k) shown the center of the circle.

By comparing equation (i) and equation (ii), we get

r^2 = 9

r = 3

`(x-3)^(2) = (x-h)^(2)`

`(x-3) = (x-h)`

`h = 3`

`(y+4)^(2) = (y-k)^(2)`

`(y+4) = (y-k)`

`k = -4`

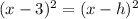
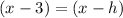
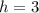
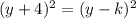
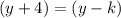
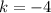
So the center of given circle is (h,k) = (3,-4)

Also, the circle is translated 5 units left, that is towards the -x-axis. Therefore h = 3 - 5 = -2

Also, the circle is translated 1 unit up, that is towards the +y-axis. Therefore k = -4 + 1 = -3

Hence, the point at which center of the image circle located is (-2, -3) so second option is correct.