Question

What is the area of the regular pentagon below

688.2 ft

850.7 ft

951.1 ft

1,376.4 ft

Answer 1

For this case we have that by definition, the polygon area shown is given by:

`A = \frac {p * a} {2}`

Where:

p: It is the perimeter

a: It is the apothem

So, the perimeter is:

`p = 5 * 20\\p = 100 \ ft`

On the other hand, the apothem is given by:

`tag (36) = \frac {10} {a}\\a = \frac {10} {tag (36)}\\a = \frac {10} {0.72654253}\\a = 13.7638191669247`

Finally, the area is:

`A = \frac {100 * 13.7638191669247} {2}\\A = 688.19096`

Rounding off we have:
`688.2 \ ft ^ 2`

Answer:

Option A

Answer 2

A

Explanation:

By definition, all sides of a regular polygon are equal in length. If you know the length of one of the sides, the area is given by the formula:

`A=(s^2\cdot n)/(4\tan (180^(\circ))/(n)),`

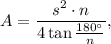
where s is the side length, n is the number of sides.

In your case, s=20 ft, n=5,so

`A=(20^2\cdot 5)/(4\tan (180^(\circ))/(5))=(400\cdot 5)/(4\tan 36^(\circ))=(500)/(0.73)\approx 688.2\ ft^2`