Question

A sample of 1,000 bacteria becomes infected with a virus. Each day, one-fourth of the bacteria sample dies due to the virus. A biologist studying the bacteria models the population of the bacteria with the function P(t) = 1,000(0.75)^t, where t is the time, in days.What is the range of this function in this context?

Answer 1

D- Any whole number such that 0<P(t)<1000

Explanation:

got it right

Answer 2

Hello!

The answer is:

The range of the function is:

Range: (0,1000]

Why?

To know the range of this function in this context, first, we need to find which is the maximum value that the function can reach.

It's true that exponential function has a range which comprehends all the real numbers greater than 0, but for the experiment, the range of the function will be all the numbers greater than 0 but less or equal than the highest value that the population of bacteria at the start of the experiment.

So, to calculate the highest population of bacteria before even it started to decrease, we need to use "t" equal to 0.

Calculating we have:

`P(t) = 1,000(0.75)^t\\\\y=1,000(0.75)^0=1000*1=1000`

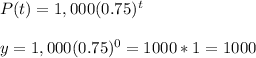
Hence, we have that the maximum value that the function can reach is 1000 units of bacteria. Meaning that the range of the function will be:

Range: (0,1000]

Have a nice day!