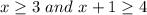Question

the sum of 2 consecutive integers is at most the difference between nine times the smaller and 5 times the larger

Answer 1

`x\geq 3 \ and \ x+1 \geq 4`

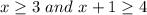
Explanation:

The question in this problem is:

The sum of 2 consecutive integers is at most the difference between nine times the smaller and 5 times the larger. What are the numbers?

First of all, let's name the first variable
`x` which is the smaller number. Accordingly, the lager number will be
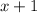`x+1` given that those numbers are consecutive. On the other hand at most conveys the idea of an inequality, which is:

`\leq \\ which \ means \ less \ than`

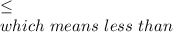
So:

1. The sum of 2 consecutive integers can be written as:

`v+(v+1)`

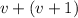
2. Nine times the smaller and 5 times the larger can be written as:

`9v-5(v+1)`

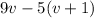
Finally, the whole statement:

The sum of 2 consecutive integers is at most the difference between nine times the smaller and 5 times the larger:

`x+(x+1) \leq 9x-5(x+1) \\ \\ x+x+1\leq 9x-5x-5 \\ \\ 2x+1 \leq 4x-5 \\ \\ 6 \leq 2x \\ \\`

`x+(x+1) \leq 9x-5(x+1) \\ \\ x+x+1\leq 9x-5x-5 \\ \\ 2x+1 \leq 4x-5 \\ \\ 6 \leq 2x \\ \\ (6)/(2) \leq (2x)/(2) \\ \\ 3 \leq x \\ \\ x\geq 3 \\ \\ and \\ \\ x+1 \geq 4`

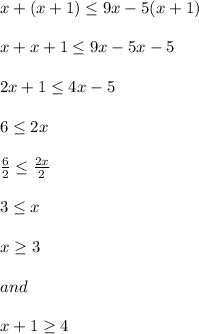
The two numbers are:

`x\geq 3 \ and \ x+1 \geq 4`