Question

1.2,3,7.5,18.75, which formula can be used to describe the sequence

Answer 1

`a_(n)=1.2 *(2.5)^(n-1)`

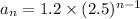
Explanation:

If we observe the given sequence, we find that the ratio of two consecutive terms is the same. i.e.

`(3)/(1.2)=2.5\\\\(7.5)/(3)=2.5\\\\ (18.75)/(7.5)=2.5`

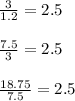
Such a sequence in which the ratio of consecutive terms remain the same is know as Geometric Sequence. Following formula is used to represent a Geometric Sequence:

`a_(n)=a_(1)*(r)^(n-1)`

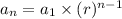
Here:

`a_(n)` is the general term. Using the value of n =1,2,3 ... will give us the term of the sequence.

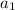`a_(1)` is the first term which is 1.2 in this case.

r represents the common ratio which is 2.5.

Using these values we get:

`a_(n)=1.2 *(2.5)^(n-1)`

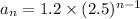
This formula can be used to represent the given sequence.