Question

What is the approximate area of the shaded sector in the circle shown below HELP FAST!!

Answer 1

ANSWER

D. 37.7cm²

Step-by-step explanation

The area of a sector of a circle is calculated using the formula,


`( \theta)/(360) * \pi \: {r}^(2)`

Where


`\theta = 30 \degree`

is the angle of the sector and

r=12cm is the radius of the circle.

We plug in the values to obtain,


`( 30)/(360) * \pi * \: {12}^(2) = 37.7 {cm}^(2)`

The correct choice is D.

Answer 2

Hello!

The answer is:

D.
`37.7cm^(2)`

Why?

To solve this problem, we need to remember the formula that defines the area of a circle.

The area of any circle is given by the following formula:

`A=\pi *r^(2)`

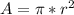
We must remember that the expression "2π" radians is equal to 360° since π radian is equal to 180°.

Then,

`(360(degrees))/(30(degrees))=12`

So,

`(360(degrees))/(12)=30(degrees)`

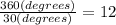
So, to calculate the area of the shaded area which represents 30° of the 360°, we need to divide the total area by 12.

`A=\pi*r^(2)=\pi*(12cm)^(2)=\pi *144=144\pi =452.39cm^(2)`

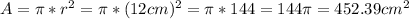
Dividing by 12, we have:

`A_{30(degrees)=(452.39cm^(2))/(12)=37.7cm^(2)`

Hence, the correct option is:

D.
`37.7cm^(2)`

Have a nice day!