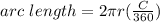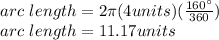Question

A central angle measuring 160 degrees intercepts an arc in a circle whose radius is 4. What is length of the arc of the circle formed by this central angel? Round the length of the arc to the nearest hundredth of unit. A. 4.19 units B. 6.28 units C. 12.57 units D. 12.75 square units

Answer 1

Answer:11.17 units

Explanation:

You can calculate the length of the arc with the formula:

`arc\ length=2\pi r((C)/(360))`

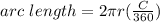
Where the radius is "r" and the central angle in degrees is "C"

Knowing the measure of the central angle and the radius:

`C=160\°\\r=4units`

Substitute them into the formula.

Then:

`arc\ length=2\pi r((C)/(360))`

`arc\ length=2\pi (4units)((160\°)/(360))\\arc\ length=11.17units`