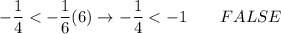Answer:
Explanation:
Convert the inequality to the form y > mx + b:
 add 2/3x to both sides
add 2/3x to both sides
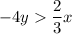 change the signs
change the signs
 divide both sides by 4
divide both sides by 4

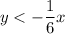
Put the coordinates of the points to the inequality and check:
for (-15, 3):

for (6, 3):
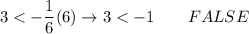
for (-3, -1/2):
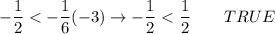
for (6, -1/4):