Question

The rectangle shown has a perimeter of 48 cm and the given area. Its length is 6 more than twice its width. Write and solve a system of equations to find the dimensions of the rectangle.

Answer 1

The length of the rectangle is 18 cm

The width of the rectangle is 6 cm

Explanation:

Let

x-----> the length of the rectangle

y----> the width of the rectangle

we know that

The perimeter of the rectangle is

`P=2(x+y)`

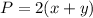
we have

`P=48\ cm`

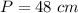
so

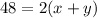`48=2(x+y)` ------> equation A

`x=2y+6` ------> equation B

Substitute equation B in equation A and solve for y

48=2(2y+6+y)

48=2(3y+6)

48=6y+12

6y=48-12

y=36/6=6 cm

Find the value of x

x=2(6)+6=18 cm

The area of the rectangle is

A=xy

A=18*6

A=108 cm^2