Question

Find the value of x

Answer 1

46.83 degrees

Explanation:

In this case, we don't have what we need to use the laws of Sines, but we can use the laws of Cosines.

If we assign the following variables to this triangle:

side a = 14

side b = 19

side c = 11

angle A = x

angle B = unknown

angle C = y

So, we're looking for the value of angle A.

The laws of Cosines (applicable to all triangles) say:

A2 = B2 + C2 -(2BC)(cos a)

If we re-arrange that we get:

`cos a = (B2 + C2 - A2)/((2BC)) = (19^(2) + 11^(2) +14^(2) )/(2 * 19 * 11) = 0.684`

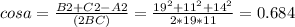
Then simply doing an inverted cos operation, we get the value of the angle... 46.83 degrees.

Answer 2

Last Option

Explanation:

We have a triangle and we know its three sides.

We want to find one of your anguos. Then we use the cosine theorem.

`c ^ 2 = a ^ 2 + b ^ 2 -2abcosx`

Where

`c = 14\\a = 11\\b = 19`

Now we solve for x from the equation

`c ^ 2 = a ^ 2 + b ^ 2 -2abcosx\\\\\\14^2 = 11^2 + 19^2 -2(11)(19)cosx\\\\14^2 -11^2 -19^2 = 2(11)(19)cosx\\\\-286=2(11)(19)cosx\\\\cosx = (-286)/(2(11)(19))\\\\x = arcos((-286)/(2(11)(19)))\\\\x = 46.8\°`