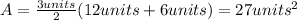Question

An isosceles trapezoid has base angles equal to 45 and bases of lengths 6 and 12. Find the area of the trapezoid.

27 sq. units
27√2 sq. units
27√3 sq. units

Answer 1

27 sq. units

Explanation:

Answer 2

First option: 27 square units.

Explanation:

The formula for calculate the area of a trapezoid is:

`A=(h)/(2)(B+b)`

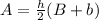
Where h is the height, B the larger base and b the smaller base.

Observe the figure of the trapezoid called ABCD. The length of the larger base (AB) is 12 units and the lenght of the smaller base (CD) is 6 units, but the height h is unknown, so you need to find it.

You can observe in the figure that two equal right triangles are formed, whose opposite side is the height "h". If you calculate the opposite side of one of those triangles, you will obtain the height of the trapezoid.

For this, you can use the identity
`tan\alpha=(opposite)/(adjacent)`.

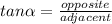Identify the opposite side, the adjacent side and the angle
`\alpha`:

`opposite=h\\adjacent=(12units-6units)/(2)=3units\\\alpha=45\°`

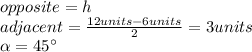
Substitute and solve for the height h:

`tan(45\°)=(h)/(3)\\(3)(tan(45\°)=h\\3units=h`

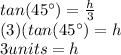
Finally substitute into
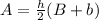`A=(h)/(2)(B+b)`:

`A=(3units)/(2)(12units+6units)=27units^2`