Write an equation for a sine curve that has the given amplitude and period, and which passes through the given point. Amplitude 5, period 6, point (2, 0)

Question

asked Sep 10, 2020 196k views

2 Answers

Kyle Dumovic · Answer 1 · 2020-09-14T05:36:12+0000

ANSWER

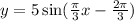
$y = 5\sin( (\pi)/(3) x - (2\pi)/(3) )$

EXPLANATION

Let the equation of the sine curve be of the form;

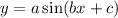
$y = a \sin(bx + c)$

where a=5 is the amplitude and period,

$(2\pi)/(b) = 6$

This implies that

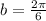
$b = (2\pi)/(6)$

$b = (\pi)/(3)$

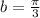
We substitute the values we got so far into our equation to obtain;

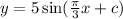
$y = 5\sin( (\pi)/(3) x + c)$

When we substitute (2,0) we obtain;

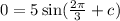
$0= 5\sin( (2\pi)/(3) + c)$

Solve for c.

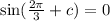
$\sin( (2\pi)/(3) + c) = 0$

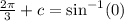
$(2\pi)/(3) + c = \sin^( - 1) (0)$

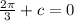
$(2\pi)/(3) + c = 0$

$c = - (2\pi)/(3)$

Hence our equation becomes

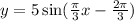
$y = 5\sin( (\pi)/(3) x - (2\pi)/(3) )$

The correct choice is D.