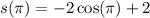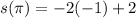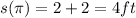If a spring is oscillating (moving) according to the velocity equation v(t) = 2sin(t) (in ft/s), then what is its displacement over its first π seconds of travel?

Question

asked Nov 5, 2020 110k views

1 Answer

Eddie Awad · Answer 1 · 2020-11-11T07:31:55+0000

ANSWER

4 ft

Step-by-step explanation

The velocity equation of the oscillating spring is given by the function.

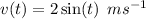
$v(t)=2 \sin(t) \: \: {ms}^( - 1)$

To find the displacement function, we need to to Integrate the velocity function.

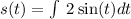
$s(t) = \int \: 2 \sin(t) dt$

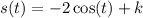
$s(t) = - 2 \cos(t) + k$

At time t=0, there was no displacement.

This implies that,

s(0) = 0

$0= - 2 \cos(0) + k$

0= - 2 + k

k = 2

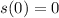
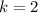
The displacement function then becomes,

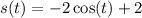
$s(t) = - 2 \cos(t) + 2$

To find the displacement over the first π seconds, we put

$t = \pi$

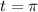
into the equation for the displacement to get,

$s(\pi) = - 2 \cos(\pi) + 2$

$s(\pi) = - 2 ( - 1) + 2$

$s(\pi) = 2 + 2 =4 ft$