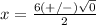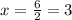Question

Given that EF and EG are tangent lines, apply the Tangent Segments Theorem to set up an equation and solve for x.

Answer 1

The value of x is 3

Explanation:

we know that

The Tangent Segment Theorem states that if from one external point, two tangents are drawn to a circle then they have equal tangent segments

so

In this problem

`EF=EG`

substitute the values

`x^(2)-4x+5=2x-4\\x^(2)-4x+5-2x+4=0\\x^(2)-6x+9=0`

Solve the quadratic equation

The formula to solve a quadratic equation of the form
`ax^(2) +bx+c=0` is equal to

`x=\frac{-b(+/-)\sqrt{b^(2)-4ac}} {2a}`

in this problem we have

`x^(2)-6x+9=0`

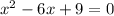
so

`a=1\\b=-6\\c=9`

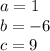
substitute in the formula

`x=\frac{6(+/-)\sqrt{-6^(2)-4(1)(9)}} {2(1)}`

`x=\frac{6(+/-)√(0)} {2}`

`x=\frac{6} {2}=3`