Using mathematical induction prove whether or not the following statement is true for all positive integers n, or show why it is false. 2+6+10+ ... +4n-2=2n^2

Question

asked Feb 2, 2020 103k views

1 Answer

Shuki Avraham · Answer 1 · 2020-02-06T06:26:06+0000

Base case: For
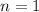n=1 , the left side is 2 and the right is
$2\cdot1^2=2$ , so the base case holds.

Induction hypothesis: Assume the statement is true for
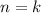n=k , that is

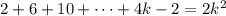
$2+6+10+\cdots+4k-2=2k^2$

We want to show that this implies truth for
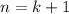n=k+1 , that

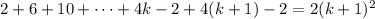
$2+6+10+\cdots+4k-2+4(k+1)-2=2(k+1)^2$

The first
terms on the left reduce according to the assumption above, and we can simplify the
k+1 -th term a bit:

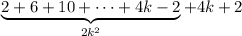
$\underbrace{2+6+10+\cdots+4k-2}_(2k^2)+4k+2$

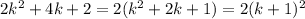
2k^2+4k+2=2(k^2+2k+1)=2(k+1)^2

so the statement is true for all
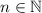$n\in\mathbb N$ .