Answer:
1) Mistakes:
The adjacent side that is next to the missing angle is not 16, so
 is incorrect.
is incorrect.
He should have used
 to find the missing angle.
to find the missing angle.
2) The correct solution is:
 ≈53°
≈53°
Explanation:
Remember that:
1)
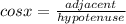
If
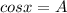 , then the angle whose cosine is A, can be calculated with the inverse function of the cosine:
, then the angle whose cosine is A, can be calculated with the inverse function of the cosine:
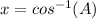
2)

If
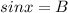 , then the angle whose sine is B, can be calculated with the inverse function of the sine:
, then the angle whose sine is B, can be calculated with the inverse function of the sine:

The mistakes that Bob made, are:
The adjacent side of the right triangle is not 16, so
 is incorrect.
is incorrect.
Knowing that the missing angle is "x", the opposite side and the hypotenuse are the known sides. Therefore, he should have used
 to find the missing angle.
to find the missing angle.
Therefore, the correct solution is:

 ≈53°
≈53°