Answer:
Option 2 - Hyperbola
Explanation:
Given : The polar equation

To find : What conic section is represented by the polar equation?
Solution :
To find the conic section first we convert the polar into Cartesian equation
We know,
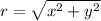 and
and



Substitute the value of r,
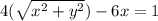
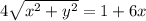
Squaring both side,
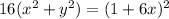
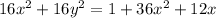
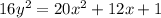
Applying completing the square we get,

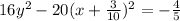
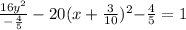
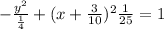
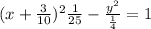
This is in the form of hyperbola equation i.e.
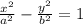
Therefore, The given conic section is a hyperbola.
Hence, Option 2 is correct.