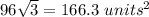Question

Find the area of a regular hexagon with a radius of 8 and an apothem of 4√3.

Round your answer to the nearest tenth.

Answer 1

The area of the regular hexagon is
`166.3\ units^(2)`

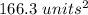
Explanation:

we know that

The regular hexagon can be divided into 6 equilateral triangles

so In this problem

The radius is equal to length side of the polygon

The area of the regular hexagon is equal to the area of six equilateral triangle

`A=6[(1)/(2)(b)(h)]`

we have

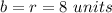`b=r=8\ units` ---> the base of each triangle is equal to the radius

`h=4√(3)\ units` ---> the height of each triangle is equal to the apothem

substitute

`A=6[(1)/(2)(8)(4√(3))]=96√(3)\ units^(2)`

`96√(3)=166.3\ units^(2)`