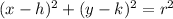Question

The circle below is the graph of which of the following equations

Answer 1

`(x-4)^(2)+(y-4)^(2)=32`

Explanation:

we know that

The equation if the circle into center radius form is equal to

`(x-h)^(2)+(y-k)^(2)=r^(2)`

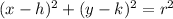
where

(h,k) is the center of the circle

r is the radius

In this problem we have

`(h,k)=(4,4)`

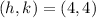
Find the radius of the circle

we know that

The distance between the center and any point that lie on the circle is equal to the radius

Let

`A(0,0),B(4,4)`

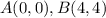
the formula to calculate the distance between two points is equal to

`d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}`

substitute the values

`r=\sqrt{(4-0)^(2)+(4-0)^(2)}`

`r=\sqrt{(4)^(2)+(4)^(2)}`

`r=√(32)\ units`

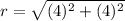
substitute in the equation of the circle

`(x-h)^(2)+(y-k)^(2)=r^(2)`

`(x-4)^(2)+(y-4)^(2)=(√(32))^(2)`

`(x-4)^(2)+(y-4)^(2)=32`