Question

Early black-and-white television sets used an electron beam to draw a picture on the screen. The electrons in the beam were accelerated by a voltage of 3.0 kV m kV; the beam was then steered to different points on the screen by coils of wire that produced a magnetic field of up to 0.67T

A

What is the speed of electrons in the beam?

B

What acceleration do they experience due to the magnetic field, assuming that it is perpendicular to their path? What is this acceleration in units of g Image for Early black-and-white television sets used an electron beam to draw a picture on the screen. The electrons in?

C

If the electrons were to complete a full circular orbit, what would be the radius?

Answer 1

A)
`3.25\cdot 10^7 m/s`

Assuming the electrons start from rest, their final kinetic energy is equal to the electric potential energy lost while moving through the potential difference
`\Delta V`:

`K=(1)/(2)mv^2 = q\Delta V`

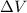where

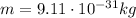`m=9.11\cdot 10^(-31)kg` is the mass of each electron

v is the final speed of the electrons

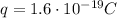`q=1.6\cdot 10^(-19)C` is the charge of the electrons

`\Delta V=3.0 kV=3000 V` is the potential difference

Solving the equation for v, the speed, we find

`v=\sqrt{(2q\Delta V)/(m)}=\sqrt{(2(1.6\cdot 10^(-19)C)(3000 V))/(9.11\cdot 10^(-31) kg)}=3.25\cdot 10^7 m/s`

B) Centripetal acceleration,
`3.82\cdot 10^4 m/s^2`, in units of g: 3898 g

When the electrons cross the region of the magnetic field, they experience a magnetic force which is perpendicular to their trajectory: therefore they start moving in a circular motion. The acceleration they experience is not tangential, but centripetal, and it is given by

`a_c = (v^2)/(r)`

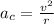
where v is the speed and r the radius of the trajectory.

We can equate the magnetic force exerted on the electrons to the centripetal force:

`qvB=ma_c`

and isolate
`a_c` to find the centripetal acceleration:

`a_c = (qvB)/(m)=((1.6\cdot 10^(-19) C)(3.25\cdot 10^7 m/s)(0.67 T))/(9.11\cdot 10^(-31) kg)=3.82\cdot 10^4 m/s^2`

And since
`g=9.81 m/s^2`, the acceleration can be rewritten as

`a_c = (3.82\cdot 10^4 m/s^2)/(9.81 m/s^2)=3898 g`

c)
`2.76\cdot 10^(10) m`

The radius of the circular trajectory can be found by using the formula for the centripetal acceleration:

`a_c = (v^2)/(r)`

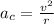
Solvign for r, we find

`r=(v^2)/(a_c)=((3.25\cdot 10^7 m/s)^2)/(3.82\cdot 10^4 m/s^2)=2.76\cdot 10^(10) m`