Question

Determine the total number of roots of each polynomial function using the factores form? F(x) = (x-6)^2(x+2)^2

Answer 1

4

Explanation:

If we perform the indicated multiplication, the highest powered x term will be 4 (as in x^4). Thus, the total number of roots of this polynomial will be 4.

Answer 2

total number of roots =4

Explanation:

the total number of roots of each polynomial function using the factored form

`F(x) = (x-6)^2(x+2)^2`

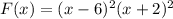
Given f(x) is in factored form, to get the roots we look at the factors and the exponents.

`(x-6)^2` has exponent 2, so we have two roots 6 and 6

like that
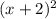`(x+2)^2` gives us two roots because it has exponent 2

So total number of roots for this polynomial function is 4