Graph for f(x) = ((2x+3)(x-6))/((x+2)(x-1))

Question

Graph for
`f(x) = ((2x+3)(x-6))/((x+2)(x-1))`

Answer 1

The graph is attached below

Explanation:

The function has three asymptotes. Before we can graph the function, we can find them.

Vertical asymptotes in the values that make the denominator zero.

The denominator becomes zero in:

`x = -2\\x = 1\\`

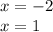
Then the vertical asymptotes are the lines

`x = -2\\x = 1\\`

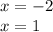
The horizontal asymptote is found using limits

`\lim_(x\to \infty)((2x+3)(x-6))/((x+2)(x-1))`

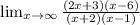
Then:

`\lim_(x\to \infty)((2x^2-12x +3x -18))/(x^2-x+2x-2)`

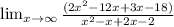
We divide the numerator and the denominator between the term of greatest exponent, which in this case is
`x ^ 2`

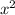
The terms of least exponent tend to 0

`\lim_(x\to \infty)((2(x^2)/(x^2)-0 +0 -0))/((x^2)/(x^2)-0+0-0)\\\\\lim_(x\to \infty)(2)/(1) = 2\\\\`

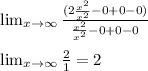
The function has a horizontal asymptote on y = 2 and has no oblique asymptote

The graph is attached below