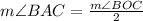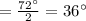Question

PLEASE HELP

In the same circle, chord AB determines a 115° arc and chord AC determines a 43° arc. Find m∠BAC.
(2 answers)

Answer 1

101 or 36 degrees

Explanation:

If you add up the measures of the arcs it is 158. That means BC is 202 degrees. Divide it by 2 to find the angle. For the second answer, remember the question did not specify if the arcs were major or minor so you can flip them around.

Answer 2

m∠BAC is 101° or 36°.

Explanation:

Given,

`m(\widehat{AB})=115^(\circ)`

`m(\widehat{AC})=43^(\circ)`

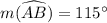
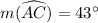
To find : The measurement of angle BAC,

Let O be the center of the circle.

Since, here we have to cases ( shown in diagram ),

In Case 1 :

`m\angle BOC = 360^(\circ)-[m(\widehat{AB})+m(\widehat{AC})]`

`=360^(\circ)-(115^(\circ)+43^(\circ))`

`=360^(\circ)-158^(\circ)`

`=202^(\circ)`

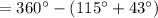
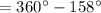
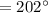
By the central angle theorem,

`m\angle BAC = (m\angle BOC)/(2)`

`=(202^(\circ))/(2)=101^(\circ)`

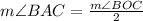
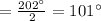
In Case 2 :

`m\angle BOC = m(\widehat{AB})-m(\widehat{AC})`

`=115^(\circ)-43^(\circ)`

`=72^(\circ)`

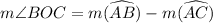
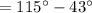
Again by the central angle theorem,

`m\angle BAC = (m\angle BOC)/(2)`

`=(72^(\circ))/(2)=36^(\circ)`