Factorization for the monomial 48x^(10)

Question

Factorization for the monomial

`48x^(10)`

Answer 1

Answer with step-by-step explanation:

We are given the following monomial and we are to factorize it:

`4 8 x ^ { 10 }`

We have a number of options that we can opt for in order to factorize the given monomial:

`( 16 x ^ 2 ) ( 3 x ^ 8 )`

or

`( 12 x ^ 5 ) ( 4 x ^ 5 )`

or

`( 24 x ^ 3 ) ( 2 x ^ 7 )`

So basically it depends how do you want to break the coefficient and the exponent in order to get a product of
`4 8 x ^ { 10 }`.

Answer 2

Some of the possible factorizations of the monomial given are:

`(16x^5)(3x^5)`

`(48x)(x^9)\\\\(4x^5)(12x^5)\\\\(16x^2)(3x^8)\\\\(2x^2)(4x^7)(6x)`

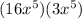
Explanation:

To factorize the monomia you need to express it as a product of two or more monomials. Therefore, you must apply the proccedure shown below:

- Descompose into prime numbers:

`48x^(10)=2*2*2*2*3*x*x*x*x*x*x*x*x*x*x`

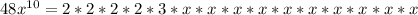
- Then, keeping on mind that, according to the Product of powers property, when you have two powers with equal base you must add the exponents, you can make several factorizations. Below are shown some of the possible factorizations of the monomial given:

`(2^4x^5)(3x^5)`

`(48x)(x^9)\\\\(4x^5)(12x^5)\\\\(16x^2)(3x^8)\\\\(2x^2)(4x^7)(6x)`