Question

I need help please..
proof it by mathematical induction
10+24+38+.......+(14n-4)=7n²+3n

Answer 1

When proving something by induction, we have to establish a base case: we must prove that our assumption

`P(n):= 10+24+38+.......+(14n-4)=7n^2+3n`

is true for
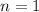`n=1`. We have

`(14\cdot 1-4) = 7\cdot 1^2+3\cdot 1 \iff 14-4 =7+3 \iff 10=10`

With the base case covered, we assume
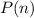`P(n)` and prove that if
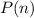`P(n)` holds, then
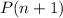`P(n+1)` follows. We have

`P(n+1):= 10+24+38+.......+(14n-4)+(14(n+1)-4)=7(n+1)^2+3(n+1)`

Rewrite this expression as

`10+24+38+.......+(14n-4) + 14n+10 = 7n^2+14n+7+3n+3`

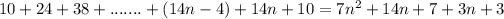
Rearrange the terms as follows:

`10+24+38+.......+(14n-4) + 14n+10 = 7n^2+3n+14n+10`

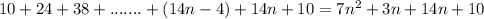
We already know (because we are assuming
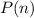`P(n)`) that

`10+24+38+.......+(14n-4)=7n^2+3n`

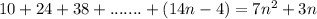
And when writing
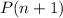`P(n+1)` we wrote this equation, adding
`14n+10` to both sides.

Recapping, we have assumed that
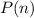`P(n)`, i.e. we have assumed that

`10+24+38+.......+(14n-4)=7n^2+3n`

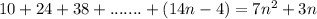
Then we showed that
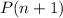`P(n+1)` can be written as

`\big(10+24+38+.......+(14n-4)\big)+14n+10=\big(7n^2+3n\big)+14n+10`

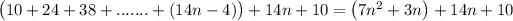
And so, if
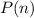`P(n)` is true,
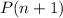`P(n+1)` must be true as well. This concludes the proof.