Question

Find the product of
(x2 + 3x + 1)(x2 + x + 2)

Answer 1

Hello!

The answer is:
`x^(4)+4x^(3)+6x^(2)+7x+2`

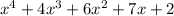
Why?

To find the product of the given expression, we need to apply the distributive property and then, group each like term.

The distributive property states that:

(a+b+c)(d+e+f)=a*d+a*e+a*f+b*d+b*e+b*f+c*d+c*e+c*f

Then, we have to group each like term. Like terms are the terms that have the same variable and exponent , for example:

`x+x+x^(2)=2x+x^(2)`

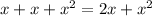
For this case, the variable "x" has two Like terms, since both have the same exponent (1), then, we add each other in order to group term.

Also, we must remember the following power property:

Product of powers property,

`a^(n)*a^(m)=a^(n+m)`

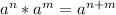
So, solving the product we have:

`(x^(2)+3x+1)(x^(2)+x+2)=x^(2)*x^(2)+x*x^(2)+2x^(2)+3x*x^(2)+3x*x+6x+x^(2)+x+2\\(x^(2)+3x+1)(x^(2)+x+2)=x^(2+2)+x^(1+2)+2x^(2)+3x^(2+1)+3x^(1+1)+6x+x^(2)+x+2\\(x^(2)+3x+1)(x^(2)+x+2)=x^(4)+4x^(3)+6x^(2)+7x+2`

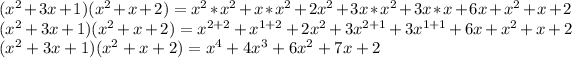
Have a nice day!

Answer 2

Answer:
`x^4+4x^3+6x^2+7x+2`

Explanation:

To solve the exercise you must apply the following proccedure:

- Apply the distributive property.

- Keep on mind that when you multiply two powers with equal base, you must add the exponents.

- Add like terms.

Therefore, you obtain the following product:

`=x^((2+2))+x^((2+1))+2x^2+3x^((1+2))+3x^((1+1))}+6x+x^(2)+x+2\\=x^4+x^3+2x^2+3x^3+3x^2+6x+x^2+x+2\\=x^4+4x^3+6x^2+7x+2`