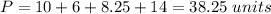Question

What is the perimeter of the trapezoid with vertices Q(8, 8), R(14, 16), S(20, 16), and T(22, 8)? Round to the nearest hundredth, if necessary. units

Answer 1

38.25

Explanation:

took the test edge

Answer 2

The perimeter of the trapezoid is
`38.25\ units`

Explanation:

we know that

The perimeter of the trapezoid is the sum of its four side lengths

so

In this problem

`P=QR+RS+ST+QT`

the formula to calculate the distance between two points is equal to

`d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}`

we have

`Q(8, 8), R(14, 16), S(20, 16),T(22, 8)`

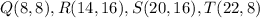
step 1

Find the distance QR

`Q(8, 8), R(14, 16)`

substitute the values in the formula

`d=\sqrt{(16-8)^(2)+(14-8)^(2)}`

`d=\sqrt{(8)^(2)+(6)^(2)}`

`d=√(100)`

`QR=10\ units`

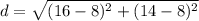
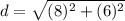
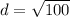
step 2

Find the distance RS

`R(14, 16), S(20, 16)`

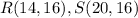
substitute the values in the formula

`d=\sqrt{(16-16)^(2)+(20-14)^(2)}`

`d=\sqrt{(0)^(2)+(6)^(2)}`

`d=√(36)`

`RS=6\ units`

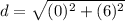
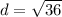
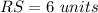
step 3

Find the distance ST

`S(20, 16),T(22, 8)`

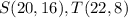
substitute the values in the formula

`d=\sqrt{(8-16)^(2)+(22-20)^(2)}`

`d=\sqrt{(-8)^(2)+(2)^(2)}`

`d=√(68)`

`ST=8.25\ units`

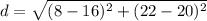
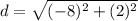
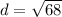
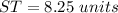
step 4

Find the distance QT

`Q(8, 8),T(22, 8)`

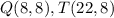
substitute the values in the formula

`d=\sqrt{(8-8)^(2)+(22-8)^(2)}`

`d=\sqrt{(0)^(2)+(14)^(2)}`

`d=√(196)`

`QT=14\ units`

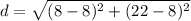
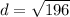
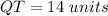
step 5

Find the perimeter

`P=10+6+8.25+14=38.25\ units`