Question

A force of 5N and a force of 8N act to the same point and are inclined at 45degree to each other. Find the magnitude and direction of the resultant force.

Answer 1

• Magnitude: 12.1 N.
• Direction: 17.0° to the 8 N force.

Step-by-step explanation

Refer to the diagram attached (created with GeoGebra). Consider the 5 N force in two directions: parallel to the 8 N force and normal to the 8 N force.

• 
  `\displaystyle F_{\text{1, Parallel}} = F_1 \cdot cos(45^\textdegree) = (5√(2))/(2)\;\text{N}`.
• 
  `\displaystyle F_{\text{1, Normal}} = F_1 \cdot sin(45^\textdegree) = (5√(2))/(2)\;\text{N}`.

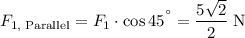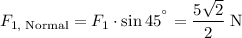The sum of forces on each direction will be the resultant force on that direction:

• Resultant force parallel to the 8 N force:
  `(8 + (5√(2))/(2))\;\text{N}`.
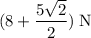• Resultant force normal to the 8 N force:
  `(5√(2))/(2)\;\text{N}`.

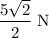Apply the Pythagorean Theorem to find the magnitude of the resultant force.

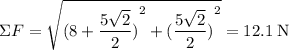`\displaystyle \Sigma F = \sqrt{{(8 + (5√(2))/(2))}^2 + {((5√(2))/(2))}^2} = 12.1\;\text{N}` (3 sig. fig.).

The size of the angle between the resultant force and the 8 N force can be found from the tangent value of the angle. Tangent of the angle:

`\displaystyle \frac{\Sigma F_\text{Normal}}{\Sigma F_\text{Parallel}} = (8 + (5√(2))/(2))/((5√(2))/(2)) \approx 0.306491`.

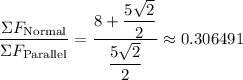Find the size of the angle using inverse tangent:

`\displaystyle \arctan{ \frac{\Sigma F_\text{Normal}}{\Sigma F_\text{Parallel}}} = \arctan{0.306491} = 17.0\textdegree`.

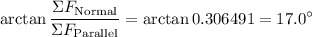In other words, the resultant force is 17.0° relative to the 8 N force.