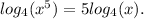ANSWER
1.
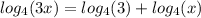
2.
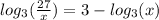
3.
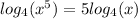
Step-by-step explanation
1. The given logarithmic expression is
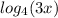
Use the product rule:
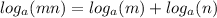
We apply this rule to obtain:
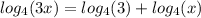
2. The given logarithmic expression is

We apply the quotient rule:
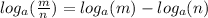
This implies that;

We simplify to get;

Apply the power rule:
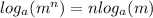
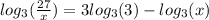
simplify;
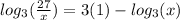
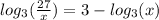
3. The given logarithmic expression is;

Apply the power rule of logarithms.
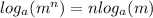
This implies that,