Question

10 points!! Please show work!!

Answer 1

Smaller x: -10

Larger x: -2

Explanation:

You are looking for where the function equals 0. So, you can set f(x) equal to 0:

f(x) =
`0=(x+6)^(2) -16`

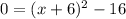
Now add 16 to both sides:

`16=(x+6)^(2)`

Now that you have a perfect square on both sides, you can take the square root of both sides. On the right, this would simply remove the exponent. On the left, you have the square root of 16, or 4. It is important to remember that this can be positive or negative (since -4 squared also equals 16).

±4 = x + 6

To find your two solutions, you have to then evaluate the equation for 4 and -4. First, with -4:

-4 = x + 6 subtract 6 from both sides

-10 = x

Now, with 4:

4 = x + 6 subtract 6 from both sides

-2 = x

And there are your two solutions. Since -10 < -2, -10 is the smaller x and -2 is the larger one.

Answer 2

Smaller x -10

Larger x -2

Explanation:

f(x) = (x+6) ^2 - 16

To find the zero's, we set the function equal to zero

0 = (x+6) ^2 - 16

Add 16 to each side

16 = (x+6) ^2 - 16 + 16

16 = (x+6)^2

Take the square root of each side

±sqrt(16) = sqrt((x+6)^2))

±4 = x+6

Subtract 6 from each side

-6±4 = x+6-6

-6±4 = x

-6 -4 = x -6+4 =x

-10 =x -2 =x

Smaller x -10

Larger x -2