Question

Explain....

A parallel plate capacitor has a capacity 80 x 10-6 when air is present between the plates. The volume between the plates is then completely filled with a dielectric slab of dielectric constant 20. The capacitor is now connected to a battery of 30 v by wires the dielectric slab is then removed. Then the charge that passes now through the wire is

Answer 1

The charge that will pass through the wire will be approx. 0.003C.

Step-by-step explanation:

Two equations are relevant to answer this question:

(1) The charge (Q) over a capacitance (C), given a voltage (U):

`Q = C\cdot U`

and

(2) the capacitance of a parallel-plate capacitor:

`C=\varepsilon (A)/(d)`

with
`\varepsilon` being the dielectric constant, A the plate area and d their distance.

We are given the capacitance when air is present (80 micro-Farad, or uF). The dielectric constant for air/vacuum is 8.84 pico-Farad per meter. Then someone sneaky slides a slab of dielectric medium with dielectric constant of 20 pF/m and connects a source of 30V. By inserting the slab, they increased the capacitance by a factor of 20/8.84=2.26, making it 2.26*80=181uF. By connecting it to the source 30V, they charged our capacitor to a charge

`Q = C\cdot V = 181\cdot 10^(-6)F\cdot 30V=5.43\cdot 10^(-3)C`

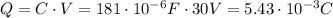
but, the sneaky person changes his mind and removes the slab, effectively changing C down to the original 80uF. There is now excess charge on the capacitor that wants to leave! The steady-state charge on the air-filled capacitor should be:

`Q_0 = C_0\cdot V = 80\cdot 10^(-6)F\cdot 30V=2.4\cdot 10^(-3)C`

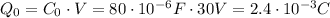
The charge that will pass through the wire will be the difference:

`Q-Q_0=(5.43-2.40)\cdot 10^(-3)C\approx 3\cdot 10^(-3)C`