Question

A tourist traveled on a motorboat against the current for 25 km. And then returned back on a raft. In the boat the tourist traveled for 10 hours less than on the raft. Find the speed of the current if the speed of the motorboat in still water is 12 km/hour.

Answer 1

2 km/h

Explanation:

Let x km/h be the speed of the current.

1. A tourist traveled on a motorboat against the current for 25 km (the current interfered), then it took him

`(25)/(12-x)\ hours.`

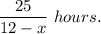
2. Then he returned back on a raft (the speed of the current is the speed of the raft), then it took him

`(25)/(x)\ hours.`

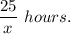
3. In the boat the tourist traveled for 10 hours less than on the raft, thus

`(25)/(12-x)+10=(25)/(x).`

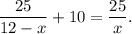
Solve this equation:

`25x+10x(12-x)=25(12-x),\\ \\25x+120x-10x^2=300-25x,\\ \\10x^2-170x+300=0,\\ \\x^2-17x+30=0,\\ \\D=(-17)^2-4\cdot 30=289-120=169,\\ \\x_(1,2)=(-(-17)\pm√(169))/(2)=2,\ 15.`

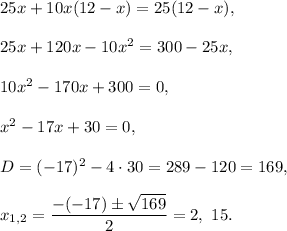
The speed of the current cannot be greater than the speed of the boat, because then tourist was not able to travel against the current. Thus, the speed of the current is 2 km/h.