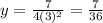Find the constant of variation for the relation and use it to write an equation for the statement. Then solve the equation.

Question

asked Sep 28, 2020 51.0k views

2 Answers

Vasilis Lourdas · Answer 1 · 2020-09-30T18:02:22+0000

Answer:

Choice C is the answer.

Explanation:

We have given that

If y varies inversely as the square of x

y ∝ 1/x²

y = k/x² eq(1)

where k is constant of variation.

As given that y = 7/4 when x = 1

7/4 = k/(1)²

7/4 = k/(1)

7/4 = k

Putting the value of k in eq(1), we have

y = 7/4x²

Now, we have to find the value of y when x = 3

y = 7/4(3)²

y = 7/4(9)

y = 7/36

Choice C is the answer.

Jerrytouille · Answer 2 · 2020-10-05T01:16:29+0000

Answer: option c

Explanation:

Based on the information given, you can write the following expression:

y=(k)/(x^2)

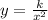
Where k is the the constant of variation

If y=7/4 when x=1, then you can substitute these values into the expression and solve for k:

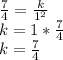
$(7)/(4)=(k)/(1^2)\\k=1*(7)/(4)\\k=(7)/(4)$

Substitute k into the expression. Then the equation is:

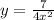
y=(7)/(4x^(2))

Substitute x=3 into the equation. Then, y is:

y=(7)/(4(3)^(2))=(7)/(36)}