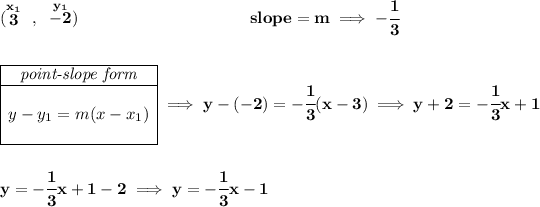Question

indicate the equation of the line that is the perpendicular bisector of the segment with endpoints (4,1) and (2,-5)

Answer 1

hmmm what would it be the bisector point of a line with those points? let's check

`\bf ~~~~~~~~~~~~\textit{middle point of 2 points } \\\\ (\stackrel{x_1}{4}~,~\stackrel{y_1}{1})\qquad (\stackrel{x_2}{2}~,~\stackrel{y_2}{-5}) \qquad \left(\cfrac{ x_2 + x_1}{2}~~~ ,~~~ \cfrac{ y_2 + y_1}{2} \right) \\\\\\ \left(\cfrac{2+4}{2}~,~\cfrac{-5+1}{2} \right)\implies \implies \left( \cfrac{6}{2}~,~\cfrac{-4}{2} \right)\implies (3,-2)`

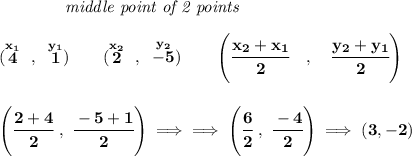
now, let's check the slope of those two points, bearing in mind that a perpendicular line will have a negative reciprocal slope to that one.

`\bf (\stackrel{x_1}{4}~,~\stackrel{y_1}{1})\qquad (\stackrel{x_2}{2}~,~\stackrel{y_2}{-5}) \\\\\\ slope = m\implies \cfrac{\stackrel{rise}{ y_2- y_1}}{\stackrel{run}{ x_2- x_1}}\implies \cfrac{-5-1}{2-4}\implies \cfrac{-6}{-2}\implies 3 \\\\[-0.35em] \rule{34em}{0.25pt}\\\\ \stackrel{\textit{perpendicular lines have \underline{negative reciprocal} slopes}} {\stackrel{slope}{3\implies \cfrac{3}{1}}\qquad \qquad \qquad \stackrel{reciprocal}{\cfrac{1}{3}}\qquad \stackrel{negative~reciprocal}{-\cfrac{1}{3}}}`

so, we're really looking for the equation of a line whose slope is -1/3 and runs through (3, -2)

`\bf (\stackrel{x_1}{3}~,~\stackrel{y_1}{-2})~\hspace{10em} slope = m\implies -\cfrac{1}{3} \\\\\\ \begin{array} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-(-2)=-\cfrac{1}{3}(x-3)\implies y+2=-\cfrac{1}{3}x+1 \\\\\\ y=-\cfrac{1}{3}x+1-2\implies y=-\cfrac{1}{3}x-1`