Question

HELP ME ASAP! PLEASEEE Elija got a job as an office clerk in 2010. At the end of every year, Elija has gotten either a raise, a promotion, or both. Elija's salary, S(t), can be determined by multiplying his starting annual salary, $24,400, by the natural logarithm of the product of 3.3 and the number of years since 2010, t.

Which of the following correctly models the situation and gives the average rate of change of Elija's salary between 2012 and 2015?

Answer 1

answer is D

Step-by-step

S (t) = 24,400 * ln (t)

Rate of Change: $7,452.50 per year

Answer 2

Option D)

`S(t) = 24400* \ln(3.3t)`

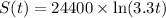
The average rate of change in Elija's salary between is $7452.50 per year.

Explanation:

We are given the following in the question:

S(t) represent the Elija's salary.

S(t) can be obtained by multiplying starting annual salary, $24,400, by the natural logarithm of the product of 3.3 and the number of years since 2010, t.

Thus, we can write:

`S(t) = 24400* \ln(3.3t)`

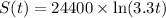
Average rate of change of function =

`\displaystyle(\delta S)/(\delta t) = (S(b)-S(a))/(b-a)`

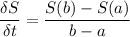
Putting b = 2015-2010 = 5, a = 2012-2010 = 2

We evaluate S(5) and S(2)

`S(t) = 24400* \ln(3.3t)\\S(5) = 24400* \ln(3.3* 5)\\S(2) = \24400* \ln(3.3* 2)`

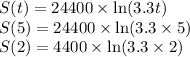
Average rate of change =

`\displaystyle\frac (S(b)-S(a))/(b-a)\\\\= (S(5)-S(2))/(5-2)\\\\=(24400(\ln(3.3* 5)-\ln(3.3* 2)))/(3)\\=7452.50`

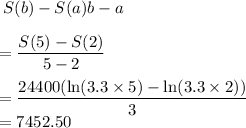
The average rate of change in Elija's salary is $7452.50 per year.