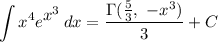Question

I have an interesting intergral that seems pretty challenging. After attempting to solve it for some time, I've come up empty handed. Can you solve this integral?

Indefinite Integral of:

`{x}^(4) { {e}^(x) }^(3)`
​

Answer 1

`\displaystyle \int {x^4e^\big{x^3}} \, dx = \sum^(\infty)_(n = 0) (x^(3n + 5))/((3n + 5)n!) + C`

`\displaystyle \int {x^4e^\big{x^3}} \, dx = (\Gamma ((5)/(3), \ -x^3))/(3) + C`

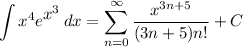
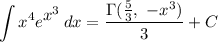
General Formulas and Concepts:

Calculus

Differentiation

• Derivatives
• Derivative Notation

Basic Power Rule:

1. f(x) = cxⁿ
2. f’(x) = c·nxⁿ⁻¹

Integration

• Integrals
• [Indefinite Integrals] Integration Constant C

Integration Property [Multiplied Constant]:
`\displaystyle \int {cf(x)} \, dx = c \int {f(x)} \, dx`

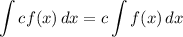
U-Substitution

Sequences

Series

Taylor Polynomials and Approximations

• MacLaurin Polynomials
• Taylor Polynomials

Power Series

• Power Series of Elementary Functions
• Taylor Series:
  `\displaystyle P(x) = \sum^(\infty)_(n = 0) (f^n(c))/(n!)(x - c)^n`

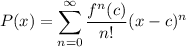
Integration of Power Series:

1. 
   `\displaystyle f(x) = \sum^(\infty)_(n = 0) a_n(x - c)^n`
2. 
   `\displaystyle \int {f(x)} \, dx = \sum^(\infty)_(n = 0) (a_n(x - c)^(n + 1))/(n + 1) + C_1`

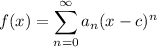
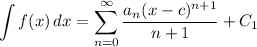
Multivariable Calculus

Gamma Functions

• 
  `\displaystyle \Gamma (s, x) = \int\limits^(\infty)_x {t^(s - 1)e^(-t)} \, dt`
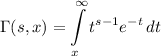
• Incomplete Gamma Functions

Explanation:

*Note:

If we are talking single-variable calculus, then we would have to write this integral as a power series.

• You can derive the power series for eˣ using Taylor Polynomials (not shown here)

If we are talking multi-variable calculus, then we could integrate this and get an "actual" value.

Single-variable Calculus

We are given the integral:

`\displaystyle \int {x^4e^\big{x^3}} \, dx`

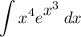
We know that the power series for
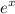`\displaystyle e^x` is:

`\displaystyle e^x = \sum^(\infty)_(n = 0) (x^n)/(n!)`

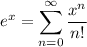
To find the power series for
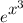`\displaystyle e^\big{x^3}` , substitute in x = x³:

`\displaystyle e^\big{x^3} = \sum^(\infty)_(n = 0) ((x^3)^n)/(n!)`

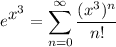
Simplify it, we have:

`\displaystyle e^\big{x^3} = \sum^(\infty)_(n = 0) (x^(3n))/(n!)`

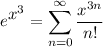
Rewrite the original function:

`\displaystyle \int {x^4e^\big{x^3}} \, dx = \int {x^4 \sum^(\infty)_(n = 0) (x^(3n))/(n!)} \, dx`

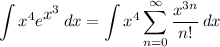
Rewrite the integrand by including the x⁴ in the power series:

`\displaystyle \int {x^4e^\big{x^3}} \, dx = \int {\sum^(\infty)_(n = 0) (x^(3n + 4))/(n!)} \, dx`

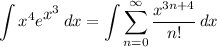
Integrating the power series, we have:

`\displaystyle \int {x^4e^\big{x^3}} \, dx = \sum^(\infty)_(n = 0) (x^(3n + 5))/((3n + 5)n!) + C`

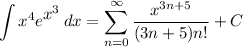
Multivariable Calculus

Let's set our variables for u-substitution:

u = x⁵ → du = 5x⁴ dx

Use u-substitution on the integral to obtain:

`\displaystyle \int {x^4e^\big{x^3}} \, dx = (1)/(5)\int {e^\big{u^{(3)/(5)}}} \, dx`

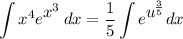
We see that the integral is an incomplete gamma function:

`\displaystyle \int {x^4e^\big{x^3}} \, dx = (1)/(5) \bigg[ \frac{5 \Gamma ((5)/(3), \ -u^\big{(3)/(5)})}{3} \bigg] + C`

Simplifying it, we have:

`\displaystyle \int {x^4e^\big{x^3}} \, dx = \frac{\Gamma ((5)/(3), \ -u^\big{(3)/(5)})}{3} + C`

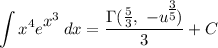
Back-substituting u will give us the final result:

`\displaystyle \int {x^4e^\big{x^3}} \, dx = (\Gamma ((5)/(3), \ -x^3))/(3) + C`