Question

Which of the following sequences are geometric? Check all that apply. PLEASE PLEASE HELP PLEASE PLEASE ASAP PLEASE PLEASE HELP PLEASE PLEASE ASAP PLEASE PLEASE HELP PLEASE PLEASE ASAP PLEASE PLEASE HELP ASAP;(

Answer 1

B and D

Explanation:

6 times 3 equals 18

18 times 3 equals 54

54 times 3 equals 162

Answer 2

Answer: The correct options are

(B) 6, 18, 54, 162, 486, . . .

(D) -4,,-2, -1, -0.5, -0.25, -0.125, . . .

Step-by-step explanation: We are given to select all the sequences that are geometric.

We know that a sequence <a(n)> is geometric is there exists a common ratio r such that

`r=(a(2))/(a(1))=(a(3))/(a(2))=~~.~~.~~.`

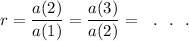
Option (A) :

Here, the given sequence is

2, 5, 8, 11, 14, 17, . . .

We see that

`(a(2))/(a(1))=(5)/(2)\\eq (a(3))/(a(2))=(8)/(5).`

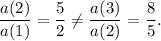
So, this sequence is not geometric and the option (A) is not correct.

Option (B) :

Here, the given sequence is

6, 18, 54, 1562, 486, . . .

We see that

`(a(2))/(a(1))=(18)/(6)=3,\\\\(a(3))/(a(2))=(54)/(18)=3,\\\\(a(4))/(a(3))=(162)/(54)=3,~~.~~.~~.~~=3.`

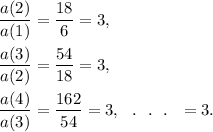
So,

`r=(a(2))/(a(1))=(a(3))/(a(2))=(a(4))/(a(3))=~~.~~.~~.`

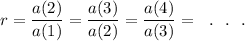
Therefore, the sequence is a geometric sequence and so the option (B) is CORRECT.

Option (C) :

Here, the given sequence is

2, 3, 5, 8, 13, 21, . . .

We see that

`(a(2))/(a(1))=(3)/(2)\\eq (a(3))/(a(2))=(5)/(3).`

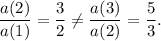
So, this sequence is not geometric and the option (C) is not correct.

Option (D) :

Here, the given sequence is

-4, -2, -1, -0.5, -0.25, -0.125, . . .

We see that

`(a(2))/(a(1))=(-2)/(-4)=(1)/(2),\\\\(a(3))/(a(2))=(-1)/(-2)=(1)/(2),\\\\(a(4))/(a(3))=(-0.5)/(-1)=(1)/(2),~~.~~.~~.`

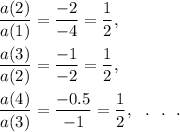
So,

`r=(a(2))/(a(1))=(a(3))/(a(2))=(a(4))/(a(3))=~~.~~.~~.~~=(1)/(2)`

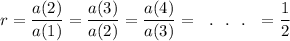
Therefore, the sequence is a geometric sequence and so the option (B) is CORRECT.

Thus, (B) and (D) are the correct options.