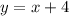The given function is
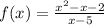
i) We factor the numerator to obtain;
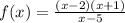
The vertical asymptote is where the denominator is zero.
V.A:

ii) The roots are the zeros of the numerator;
Roots:
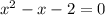
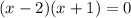
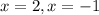
iii) At y-intercept
 .
.
Put
 into the function and solve.
into the function and solve.
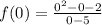
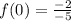
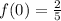
Y-int:

iv) Horizontal asymptote.
This is an improper rational function.
It has no horizontal asymptote.
v) Holes:
The given rational function has no common factors in both the numerator and the denominator.
Therefore the function has no holes.
6) For oblique Assymptote, we divide using lond division or synthetic division;
1 -1 -2
5| 5 20
1 4 18
The quotient is
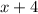
The oblique asymptote is