Question

Use the definition of continuity and the properties of limits to show that (Picture Provided Below)

Answer 1

`Lim_(x \to 5)f(x)=f(5)`.

Explanation:

The given function is

`f(x)=(x^2-49)/((x^2+6x-7)(x^2+14x+49))`.

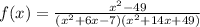We can factor an rewrite for easy evaluation;

`f(x)=((x-7)(x+7))/((x-1)(x+7)(x+7)^2)`.

`f(x)=((x-7))/((x-1)(x+7)^2)`.

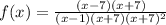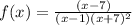Let us plug in 5.

`f(5)=((5-7))/((5-1)(5+7)^2)`.

`f(5)=(-2)/(576)`.

`f(5)=-(1)/(288)`.

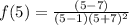Let us find the Left Hand Limit;

`Lim_(x \to 5^-)f(x)=((5-7))/((5-1)(5+7)^2)=-(1)/(288)`.

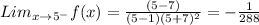Now the Right Hand Limit;

`Lim_(x \to 5^+)f(x)=((5-7))/((5-1)(5+7)^2)=-(1)/(288)`.

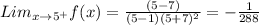Since the One-Sided Limits exist and are equal;

`Lim_(x \to 5)f(x)=((5-7))/((5-1)(5+7)^2)=-(1)/(288)`.

We have shown that;

`Lim_(x \to 5)f(x)=f(5)`.

This is the definition of continuity.

Hence f(x) is continuous at x=5