Hello!
The answer is: The mistake was in the second expression.
The second expression should be the follow:
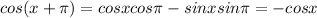
Why?
The students are working with a cosine identity, cosine sum.
According to the theorem, cosine of a sum will be:

Where, for this case:

So, substituting we have:

So, the mistake was in the second step expression.
The expression should have been:

But why the result was correct even using a wrong expression?
The answer to that question is based on the value of sin(π) which is equal to 0.
Have a nice day!