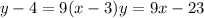For each of these questions, you need to find the derivative
 or
or
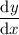 . The slope of the tangent to these curves at the point
. The slope of the tangent to these curves at the point
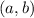 is the value of
is the value of
 when
when
 and
and
 . It's also important to know that if the slope of a line is
. It's also important to know that if the slope of a line is
 , then the slope of any line normal/perpendicular to this line is
, then the slope of any line normal/perpendicular to this line is
 .
.
###
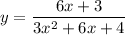
The derivative is

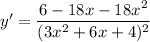
When
 , we get a slope of
, we get a slope of
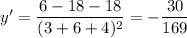
###
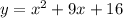
The derivative is
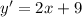
and so the tangent line at (1, 9) has slope
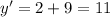
The line normal to this has slope
 . The point-slope and slope-intercept forms of this line are
. The point-slope and slope-intercept forms of this line are
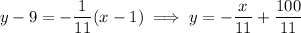
###
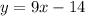
The derivative is
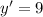
so the slope of any line tangent to the curve is 9. The line that passes through (3, 4) is