Answer:
The zeros of the given expression at x = -1.6 and x = 2.6
Explanation:
Given: -x^2 + x + 4
To find the real zeros set the expression equal to zero and solve for x.
-x^2 + x + 4 = 0
This cannot be factored.
Let's use the quadratic formula and find the solutions.
Formula x =

Here a = -1, b = 1 and c = 4 from the given expression.
Now let's plug in these values in the above formula, we get
x =

x =
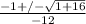
x = (-1 +/-
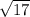 )/-2 [√17 = 4.1]
)/-2 [√17 = 4.1]
x = (-1 + 4.1)/ -2 and x = (-1 -4.1)/-2
x = 3.1/-2 and x = -5.1/-2
x = -1.55 and x = 2.55
When we round off to the nearest tenths place, we get
x = -1.6 and x = 2.6
Therefore, the zeros of the given expression at x = -1.6 and x = 2.6.
Hope this will helpful.
Thank you.