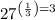Question

Rewrite the logarithmic equation as an exponential equation: log27 3=1/3

Answer 1

3 = 27^1/3

Explanation:

log27 3=1/3

Raise each side to the base of 27

27^log27 3=27^1/3

3 = 27^1/3

Answer 2

`27^\left((1)/(3)\right)=3`

Explanation:

Given logarithmic equation is

`\log_(27)\left(3\right)=(1)/(3)`

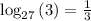
Question says to rewrite the given logarithmic equation as an exponential equation.

so we can apply transformation formula :

`\log_(b)\left(c\right)=a => c=b^a`

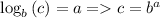
Using this formula, given problem can be transformed into exponential equation as:

`\log_(27)\left(3\right)=(1)/(3) => {27}\left((1)/(3)\right)=3`

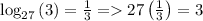
Hence final answer is
`27^\left((1)/(3)\right)=3`