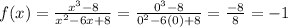F(x) = (x^(3-8) )/(x^(2) -6x+8) What is the Domain: Holes: VA: HA: OH: Roots: Y-Intercept

Question

`F(x) = (x^(3-8) )/(x^(2) -6x+8)`

What is the
Domain:
Holes:
VA:
HA:
OH:
Roots:
Y-Intercept

Answer 1

• Domain: All the real values except x = 2 and x = 4: R - {2, 4}
• Holes: x = 2
• VA, vertical asymptores: x = 4
• HA: horizontal asymptotes: there are not horizontal asymptotes
• OA: oblique asymptotes: x + 6 [note that OH does not stand for any known feature, and so it is understood that it was intended to write OA]
• Roots: x = 2
• Y-intercept: -1

Explanation:

1. Given:

`f(x)=(x^3-8)/(x^2-6x+8)`

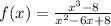
• Note that the number 8 in the numerator is not part of the power.

• Type of function: rational function

2. Domain: is the set of x-values for which the function is defined.

The given function is defined for all x except those for which the denominator equals 0.

• Denominator: x² -6x + 8 = 0

• Solve for x:

Factor. (x - 4 )(x - 2) = 0

Zero product property: (x - 4) = 0 or (x - 2) = 0

x - 4 = 0 ⇒ x = 4

x - 2 = 0 ⇒ x = 2

• Domain:

All the real values except x = 2 and x = 4: x ∈ R / x ≠ 2 and x ≠ 4.

3. Holes:

The holes on the graph of a rational function are at those x-values for which both the numerator and denominator are zero.

• Find the values for which the numerator is zero:

Numerator: x³ - 8 = 0

Factor using difference of cubes property:

a³ - b³ = (a - b)(a² + ab + b²)

x³ - 8 = (x - 2)(x² + 2x + 4) = 0

Zero product property: (x - 2)(x² + 2x + 4) = 0

x - 2 = 0 ⇒ x = 2

x² + 2x + 4 = 0 (this has not real solution)

• The values for which the denominator is zero were determined above: x = 2 and x = 4.

• Conclusion: for x = 2 both numerator and denominator equal 0, so this is a hole.

4. VA: Vertical asymptotes.

The vertical asymptotes on the graph of a rational function are the vertical lines for which only the denominator (and not the numerator) equals zero.

• In the previous part it was determined that happens when x = 4.

5. HA: Horizontal asymptotes.

In rational functions, if the numerator is a higher degree polynomial than the denominator, there is no horizontal asymptote.

6. OA: oblique asymptotes

• Find the quotient and the remainder.

x + 6

_______________

x² - 6x + 8 ) x³ + 0x² + 0x - 8

- x³ + 6x² - 8x

___________

6 x² - 8x - 8

- 6x² + 36x - 48

_____________

28x - 56

Result: (x + 6) + (28x - 56) / (x² - 6x + 8)

• Find limit x → ∞

`\lim_(x \to \infty)(x + 6) + (28x-56)/(x^2-6x+8)=x+6`

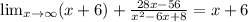
7. Roots:

Roots are the values for which f(x) = 0.

That happens when the numerator equals 0, and the denominator is not 0.

As determined earlier: x³ - 8 = 0 ⇒ x = 2.

8. Y-Intercept

The y-intercepts of any function are the y-values when x = 0

• Substitute x = 0 into the function:

`f(x)=(x^3-8)/(x^2-6x+8)=(0^3-8)/(0^2-6(0)+8)}=(-8)/(8) =-1`