Question

The length of the base of a rectangle prism is 3 feet and its width is 2 feet. The length of the diagonal of the prism is 6 feet. What is the height of the prism to the nearest tenth a foot?

Answer 1

4.8 feet

Explanation:

Since length and width of base is 3 and 2 respectively, we find the diagonal of the base with pythagorean theorem.

`3^2+2^2=h^2\\9+4=h^2\\13=h^2\\h=√(13)`

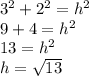
This hypotenuse is the base of a triangle with height as the height of the prism and hypotenuse being the hypotenuse of the prism.

So we can again use pythagorean theorem to solve for the height of the prism (let height of prism be x)

`(√(13) )^2+x^2=6^2\\13+x^2=36\\x^2=36-13\\x^2=23\\x=√(23)`

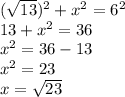
To the nearest tenth, height is 4.8 feet