Question

a planet has been detected in a circular orbit around the star Rho1 Cancri with an orbital radius equal to 1.65 x 10^10 m. the orbital period of this planet is approximately 14.5 days which is the approximate mass of the star pho1 cancri

Answer 1

Approximately
`1.69 * 10^(30)\; \rm kg`.

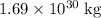Step-by-step explanation:

Deduction of the formula

Let
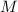`M` and
`m` denote the mass of the star and the planet, respectively.

Let
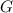`G` denote the constant of universal gravitation (
`G \approx 6.67408 * 10^(-11)\; \rm m^(3) \cdot kg^(-1)\cdot s^(-2)`.)

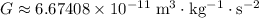Let
`r` denote the orbital radius of this planet (assuming that
`r\!` is constant.) The question states that
`r = 1.65 * 10^(10)\; \rm m`.

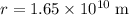The size of gravitational attraction of the star on this planet would be:
`\displaystyle (G \cdot M \cdot m)/(r^(2))`.

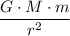If attraction from the star is the only force on this planet, the net force on this planet would be
`\displaystyle (G \cdot M \cdot m)/(r^(2))`.

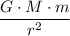Let
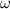`\omega` denote the angular velocity of this planet as it travels along its circular orbit around the star. The size of
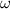`\omega\!` could be found from the period
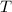`T` of each orbit:
`\omega = (2\, \pi) / T`.

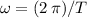In other words, this planet of mass
`m` is in a circular motion with radius
`r` and angular velocity
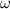`\omega`. Therefore, the net force on this planet should be equal to
`m \cdot \omega^2 \cdot r`.

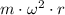Hence, there are two expressions for the net force on this planet:

• 
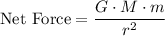  `\text{Net Force} = \displaystyle (G \cdot M \cdot m)/(r^(2))` from universal gravitation, and
• 
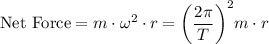  `\displaystyle \text{Net Force} = m \cdot \omega^2 \cdot r = {\left((2\pi)/(T)\right)}^(2) m \cdot r` from circular motion.

Equate the right-hand side of these two equations:

`\displaystyle (G \cdot M \cdot m)/(r^2) = {\left((2\pi)/(T)\right)}^(2)\, m \cdot r`.

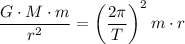Simplify this equation and solve for
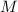`M`, the mass of the star:

`\displaystyle M = \frac{{(2\pi / T)}^2 \cdot r^3}{G}`.

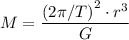Notice that
`m`, the mass of the planet, was eliminated from the equation. That explains why this question could be solved without knowing the exact mass of the observed planet.

Actual Calculations

Convert the orbital period of this star to standard units:

`\begin{aligned}T &= 14.5\; \text{day} * \frac{24\; \text{hour}}{1\; \text{day}} * \frac{3600\; \text{second}}{1\; \text{hour}} \\ & = 1.2528 * 10^(6)\; \rm \text{second}\end{aligned}`.

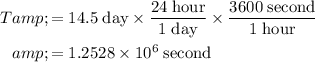Calculate the mass of the star:

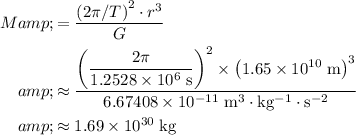`\begin{aligned} M &= \frac{{(2\pi / T)}^2 \cdot r^3}{G} \\ &\approx \frac{\displaystyle {\left((2\pi)/(1.2528 * 10^(6)\; \rm s)\right)}^(2) * \left(1.65 * 10^(10)\; \rm m\right)^(3)}{6.67408 * 10^(-11)\; \rm m^(3)\cdot kg^(-1) \cdot s^(-2)}\\ &\approx 1.69 * 10^(30)\; \rm kg\end{aligned}`.