Question

Find the sum of the geometric sequence.

1 divided by 3, 2 divided by 3, 4 divided by 3, 8 divided by 3, 16 divided by 3

Answer 1

`(31)/(3)`

Explanation:

the formula for sums of geometric sequence (pls don't use what the other person said, it worked this time with the correct answer but it won't with others - that was just a coincidence!)

`S_n=a_1((1-r^n))/((1-r))`

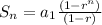
a1 = 1/3 since that's the first term

r = you divide the second term by the first term so 2/3 divided by 1/3 which is 2

n = the total number of numbers in the geometric sequence we're currently given so if you count there's 5

plug it all in and solve like normal fractions!

and you get 31/3

Answer 2

`(31)/(3)`

Explanation:

We are given the following geometric sequence and we are to find its sum:

`(1)/(3) + (2)/(3) + (4)/(3) + (8)/(3) + (16)/(3)`

For this, we just simply need to add these fractions by taking their LCM.

Since the denominator is same for all the fractions in the geometric sequence, we can take the same denominator and add all the numbers in the numerator to get:

`\frac {1 + 2 + 4 + 8 + 16 } {3}`
`= (31)/(3)`